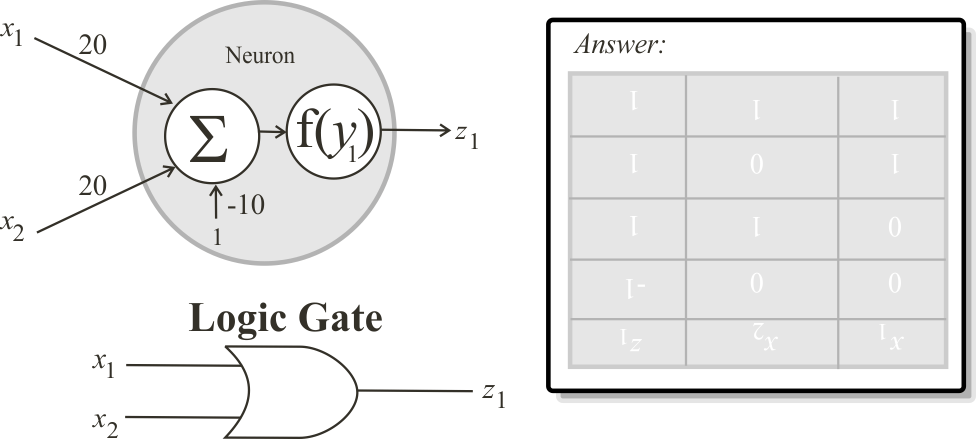
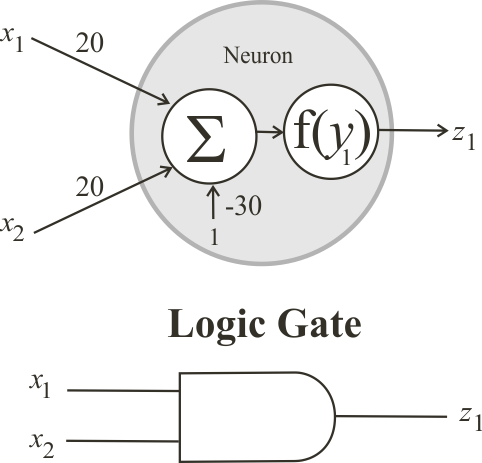
New Project click the button to create a new project called Or and write the code shown below.
New Project click the button to create a new project called Or and write the code shown below. Run click the button to execute the code. If you do not have any errors, the variables x, W and z will be displayed in the variable list. Click on z to review your results.
Run click the button to execute the code. If you do not have any errors, the variables x, W and z will be displayed in the variable list. Click on z to review your results.